Day 13: Largest Rectangle in Histogram: stack - leetcode - Python3

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

 

Example 1:

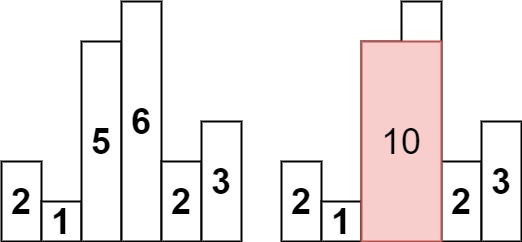
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

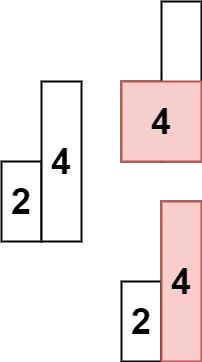
Input: heights = [2,4]
Output: 4

 

Constraints:

• 1 <= heights.length <= 105
• 0 <= heights[i] <= 104

SOLUTION:

class Solution:

    def largestRectangleArea(self, heights: List[int]) -> int:

        stack: List[int] = []

        maxarea: int = 0

        for i, h in  enumerate(heights):

            start = i

            while stack and stack[-1][1] > h:

                index, height= stack.pop()

                maxarea = max(maxarea, height * (i-index))

                start = index

           

            stack.append((start, h))

       

        for i, h in stack:

            maxarea = max(maxarea, h * (len(heights)-i) )

        return maxarea

   

Time Complexity: O(n) ->The for loop iterates over the list heights once. The while loop iterates over the stack at most once for each bar. Therefore, the total time complexity of the code is O(n).

Space Complexity: O(n) -> The stack can store at most n elements, where n is the number of bars in the histogram. Therefore, the space complexity of the code is O(n).

How it works:

1. The for loop iterates over the list heights. For each iteration, the current bar is stored in the variable h.
2. The variable start is initialized to the current index i.
3. The while loop checks if the stack is not empty and the top bar on the stack is taller than the current bar. If it is, we pop the top bar off the stack and update the variable start to the index of the popped bar.
4. The stack.append((start, h)) line appends the current index i and the current bar h to the stack.
5. The for loop iterates over the stack. For each iteration, the current index and height are stored in the variables i and h.
6. The maxarea = max(maxarea, h * (len(heights)-i) ) line calculates the area of the rectangle formed by the current bar and the bars that are stacked below it.
7. The return maxarea line returns the maximum area found.

The algorithm works by maintaining a stack of indices of the bars that form the top of the largest rectangle. The stack is initialized with the index of the first bar. For each subsequent bar, we check if it is taller than the top bar on the stack. If it is, we pop the top bar off the stack and add the new bar to the stack. We continue this process until we reach the end of the list.

Once we have processed all of the bars, we can calculate the area of the largest rectangle by multiplying the height of the top bar on the stack by the width of the rectangle. The width of the rectangle is the number of bars that are stacked below the top bar.